7 強連通元件

對於一個無向圖來說，如果我們把一個極大連通的子圖找出來（極大在這邊的定義是，無論再增加任何一個點，都沒辦法讓現在的子圖連通），那麼這個極大連通的子圖就被我們稱為連通元件。

對於有向圖來說，其連通的定義是單方向的，因此有分為弱連通 (weakly connected) 以及強連通 (strongly connected)。

弱連通：只要對於任意兩個點 u 和 v，至少有 "u 能走得到 v" 或 "v 能走得到 u”，就稱為弱連通。
強連通：對於任意兩個點 u 和 v，必須同時滿足 “u 能走得到 v” 以及 “v 能走得到 u”。

由於 「u 和 v 能夠互相走得到」這樣的定義可以想像成「u 和 v 等價」，我們可以將一張圖的所有頂點劃分成許多能夠互相走得到的等價類 (equivalence classes)。換句話說，在一張有向圖中，可以合理地定義極大強連通子圖，我們稱之為強連通元件 (strongly connected component, SCC)。

7.1 找出強連通元件的 Kosaraju 演算法

方法其實很酷，也很簡單，步驟如下：

• 第一步：對原本的圖做一次 DFS，並且將每個節點依照 DFS 結束拜訪的時間由晚到早重新排列順序。
• 第二步：把所有的邊反過來，依照重新排列的順序做一次 DFS。這步每一次的 DFS 找出來的樹，上面的點都屬於同一個強連通元件。

比方說，考慮下面這張圖以及做完第二步以後得到的強連通元件們(用同一種顏色表示)

7.2 一些應用

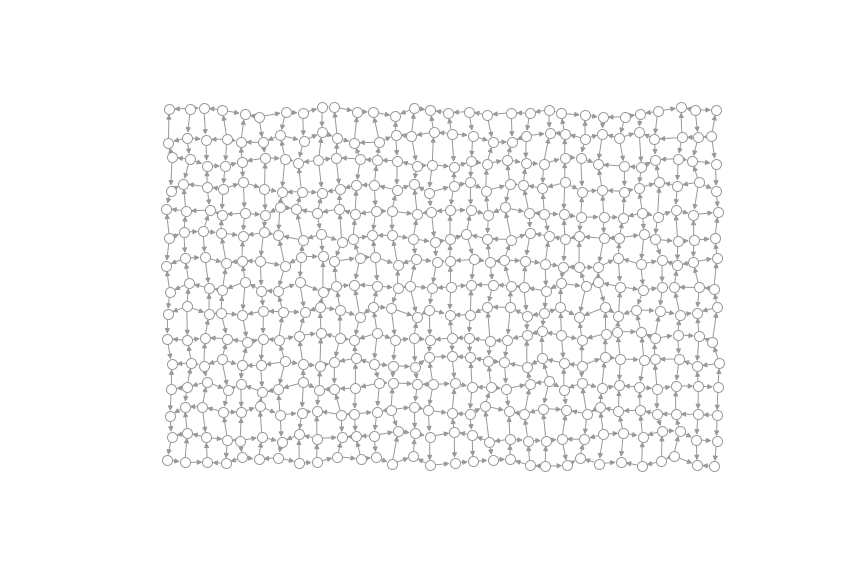
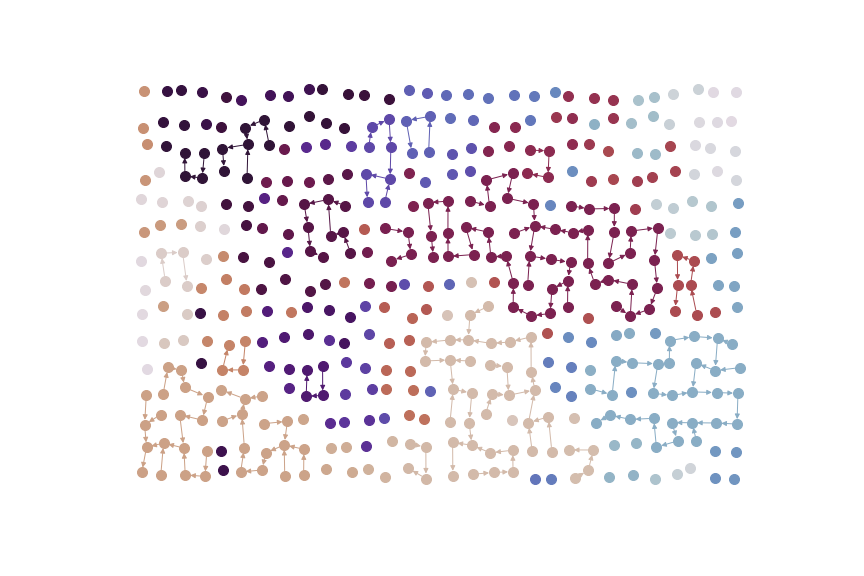
有一些圖論的問題都可以藉由先找出強連通元件以後，把這些強連通元件全部縮起來。這麼一來，這個圖就會變成有向無環圖 (directed acyclic graph, DAG)。在這樣的圖上就可以定義拓樸排序，很多問題就可以迎刃而解啦。也可以試試看隱寫術，把一張黑白的圖用強連通元件的方式藏起來，只要計算強連通元件就可以復原整張圖的概念。

7.X 冷笑話

為什麼上面那兩張圖都長得很像？因為它們都是有像圖啊。